
где а = 0, 1.
Например, число 11001110112 двоичной системы счисления в соответствии с формулой (2.4) можно представить в виде: 1 · 2 + 1 · 2 + 0 · 2 + 0 · 2 + 1 · 2 + 1 · 2 + 1 · 2 + 0 · 2 + 1 · 2 + 1 · 2.
Достаточно широко при компьютерной обработке информации применяются восьмеричная и шестнадцатеричная системы счисления, которые используются, например, для обозначения адресов расположения данных в памяти компьютера и т. д.
Соотношение (2.2) для восьмеричной и шестнадцатеричной системы счисления соответственно примет вид (2.5) и (2.6) :

где а = 0, 1, 2, 3…, 7.
Например, число 14738 восьмеричной системы счисления в соответствии с (2.5) примет вид: 1 · 8 + 4 · 8 + 7 · 8 + 3 · 8.

где а = 0, 1, 2, 3…, 9, A, B, C, D, E, F.
В шестнадцатеричной системе счисления используется шестнадцать цифр, из которых десять цифр арабские (0, 1, 2, 3, 4, 5, 6, 7, 8, 9), а остальные цифры (10, 11, 12, 13, 14, 15) обозначаются буквами латинского алфавита (А = 10, В = 11, С = 12, D = 13, E = 14, F = 15).
Например, число 33B16 шестнадцатеричной системы счисления, в соответствии с (2.6) примет вид: 3 · 16 + 3 · 16 + В · 16(В = 11).
При операциях с числами, представленными в различных системах счисления, необходимо указывать систему счисления числа, используя нижний индекс, например: 82710 – число 827 в десятичной системе; 11001110112 – число 1100111011 в двоичной системе; 14738 – число 1473 в восьмеричной системе; 33B16 – число 33В в шестнадцатеричной системе счисления.
Преобразование чисел, представленных в двоичной, восьмеричной и шестнадцатеричной системах счисления, в десятичную осуществляется достаточно просто. Для этого необходимо записать число в развернутой форме в соответствии с выражением (2.1) и вычислить его значение. Например:
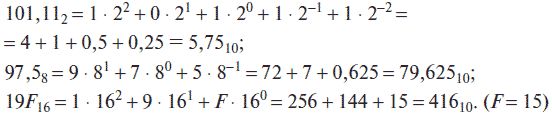
Преобразование чисел, представленных в десятичной системе счисления, в двоичную, восьмеричную и шестнадцатеричную системы счисления – более сложная процедура, которая может осуществляться различными способами: деления, умножения, вычитания и т. д. При этом необходимо учитывать, что способы перевода целых десятичных чисел и правильных дробей будут различаться. Для перевода целого десятичного числа, например 5310, в двоичную систему можно использовать способ деления, а десятичной правильной дроби, например 0,7510, в двоичную систему – способ умножения. Результаты действий отобразим в соответствующих табл. 2.1 и 2.2.
Таблица 2.1

Таким образом, 5310 = 1101012.
Таблица 2.2
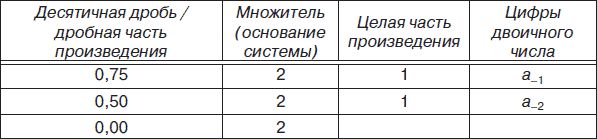
Таким образом, 0,7510 = 0,112.
Перевод чисел из одной системы счисления в другую достаточно просто реализуется с помощью компьютерных программ Калькулятор и MS Excel. Однако следует заметить, что данные программы осуществляют перевод только целых чисел.
Преобразуем число AF16с помощью компьютерного калькулятора в двоичную, восьмеричную и десятичную системы счисления. Запустим программу Калькулятор с помощью команды: [Кнопка Пуск – Программы – Стандартные – Калькулятор]. После запуска программ выполним команду: [Вид – Инженерный]. У калькулятора имеется четыре опционные кнопки, расположенные слева вверху под индикатором вывода результата вычислений. При активизации кнопки Hex осуществляется преобразование числа, отображаемого в поле ввода, и результата вычислений калькулятора в шестнадцатеричную систему счисления, Dec – в десятичную, Oct – в восьмеричную, Bin – в двоичную систему счисления. Активизируем кнопку Hex и введем число АF16. Последовательно переключая кнопки Bin, Oct и Dec, получим следующие результаты: АF16 = 101011112 = 2578 = 17510. На рис. 2.5 показан результат преобразования числа AF16в число 2578.

Рис. 2.5. Программа "Калькулятор"
Последовательность действий при преобразовании шестнадцатеричного числа AF16в двоичную, восьмеричную и десятичную системы счисления с помощью программы MS Excel аналогична преобразованию числа 1997 в римскую систему счисления, но здесь необходимо учесть, что вместо функции "Римское" необходимо использовать функции "ШЕСТН.В.ДВ", "ШЕСТН.В.ВОСЬМ", "ШЕСТН.В.ДЕС" категории "Инженерные" (см. рис. 2.2).
2.2. Арифметические операции над числами, представленными в различных системах счисления
Арифметические операции во всех позиционных системах счисления выполняются по одним и тем же правилам. Для проведения арифметических операций над числами, представленными в различных системах счисления, необходимо предварительно преобразовать их в одну систему счисления и учесть то, что перенос в следующий разряд при операции сложения и заем из старшего разряда при операции вычитания определяется величиной основания системы счисления.
Арифметические операции в двоичной системе счисления основаны на таблицах сложения, вычитания и умножения одноразрядных двоичных чисел.
При сложении двух единиц происходит переполнение разряда и производится перенос единицы в старший разряд, при вычитании 0–1 производится заем из старшего разряда, в таблице "Вычитание" этот заем обозначен 1 с чертой над цифрой.

Ниже приведены примеры выполнения арифметических операций над числами, представленными в различных системах счисления:
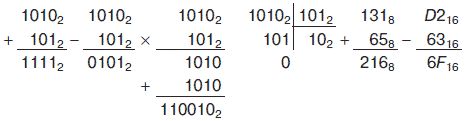
Арифметические операции над целыми числами, представленными в различных системах счисления, достаточно просто реализуются с помощью программ Калькулятор и MS Excel.
2.3. Представление чисел в компьютере
Числовые данные обрабатываются в компьютере в двоичной системе счисления. Числа хранятся в памяти компьютера в двоичном коде, т. е. в виде последовательности нулей и единиц, и могут быть представлены в формате с фиксированной или плавающей запятой.
Целые числа хранятся в памяти в формате с фиксированной запятой. При таком формате представления чисел для хранения целых неотрицательных чисел отводится регистр памяти, состоящий из восьми ячеек памяти (8 бит). Каждому разряду ячейки памяти соответствует всегда один и тот же разряд числа, а запятая находится справа после младшего разряда и вне разрядной сетки. Например, число 110011012 будет храниться в регистре памяти следующим образом: