
где Р0, P1 – вероятность достижения цели соответственно до и после получения информации.
В качестве единицы измерения (меры) количества информации, определяющей ее ценность, может быть принят 1 бит (при основании логарифма, равном 2), т. е. это такое количество полученной информации, при котором отношение вероятностей достижения цели равно 2.
Рассмотрим три случая, когда количество информации, определяющее ее ценность, равно нулю и когда она принимает положительное и отрицательное значение.
Количество информации равно нулю при Р0 = Р1, т.е. полученная информация не увеличивает и не уменьшает вероятность достижения цели.
Значение информации является положительной величиной при P1 > P0, т. е. полученная информация уменьшает исходную неопределенность и увеличивает вероятность достижения цели.
Значение информации является отрицательной величиной при P1 < P0, т. е. полученная информация увеличивает исходную неопределенность и уменьшает вероятность достижения цели. Такую информацию называют дезинформацией.
Дальнейшее развитие данного подхода базируется на статистической теории информации и теории решений. При этом кроме вероятностныхарактеристик достижения цели после получения информации вводятся функции потерь и оценка полезности информации производится в результате минимизации функции потерь. Максимальной ценностью обладает то количество информации, которое уменьшает потери до нуля при достижении поставленной цели [1].
Упражнения для самостоятельного выполнения
1. Преобразовать формулу (1.1) к виду (1.2) для частного случая, когда события равновероятны (pi = 1/N).
2. Доказать, что количество информации, которое мы получаем, достигает максимального значения, если события равновероятны.
3. По каналу связи передается пять сообщений, вероятность получения первого сообщения составляет 0,3; второго – 0,2; третьего – 0,14, а вероятности получения четвертого и пятого сообщений равны между собой. Какое количество информации мы получим после приема одного из сообщений?
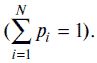
4. Совершаются два события. При каких вероятностях этих событий мы получим минимальное и максимальное количество информации?
5. Какое количество информации несет в себе сообщение о том, что нужная вам компьютерная программа находится на одной из семи дискет?
6. С помощью компьютерного калькулятора заполнить пропуски числами:
а) 2 Кбайт = ___ байт = ___ бит;
б) ___ Гбайт = 2357 Мбайт = ___ Кбайт;
в) ___ Кбайт = ___ байт = 14567 бит;
г) 3 Гбайт = __ Мбайт = ___ Кбайт;
д) ___ Тбайт = 8 Гбайт = ___ Мбайт.
7. Используя программу Excel реализовать таблицы для автоматического расчета пропущенных значений, указанных в упражнении 6.
8. Определить информационную емкость буквы в русском и латинском алфавитах.
9. Сколько символов содержит сообщение, если его информационный объем составляет 1,25 Кбайта и мощность алфавита, с помощью которого записано сообщение, равна 32?
10. Опытный пользователь компьютера может вводить в минуту 110 знаков. Мощность алфавита, используемого в компьютере, равна 256. Какое количество информации в байтах может ввести пользователь в компьютер за 1 и 1,5 минуты?
11. Установить качественную зависимость между мощностью алфавита, сообщением, составленным из символов алфавита, и его информационным объемом.
12. Определить количество информации, определяющее ее ценность, если вероятность достижения цели до получения информации равна 0,5, а после получения информации – 0,3.
Глава 2
Кодирование информации с помощью систем счисления
2.1. Системы счисления
Для записи информации о количестве объектов материального мира используются числа, которые разделяются по определенным признакам. На рис. 2.1 представлена классификация чисел по групповому признаку, когда в каждую группу входят числа, обладающие определенными свойствами.
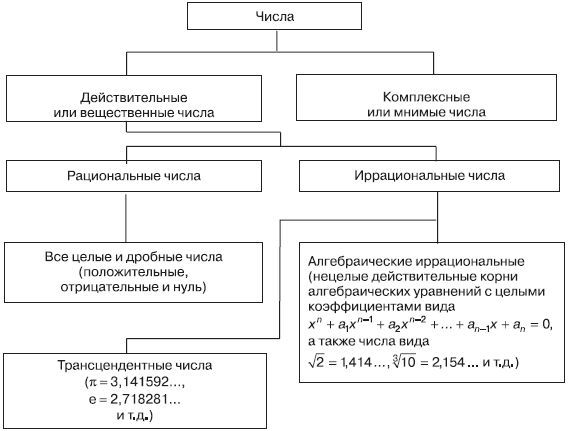
Рис. 2.1. Классификация чисел
Числа записываются с использованием особых знаковых систем, которые называются системами счисления, в них числа записываются по определенным правилам с помощью символов некоторого алфавита, называемых цифрами.
Все системы счисления делятся на два вида: позиционные и непозиционные. В позиционных системах счисления значение цифры зависит от ее положения в числе, в непозиционных – не зависит. Самой распространенной из непозиционных систем является римская. В качестве цифр в римской системе используются следующие символы: I (1), V (5), X (10), L (50), С (100), D (500), М (1000). Значение цифры в этой системе не зависит от ее положения в числе. Величина числа в римской системе определяется как сумма и разность цифр в числе. Если меньшая цифра стоит слева от большей, то она вычитается, если справа – прибавляется.
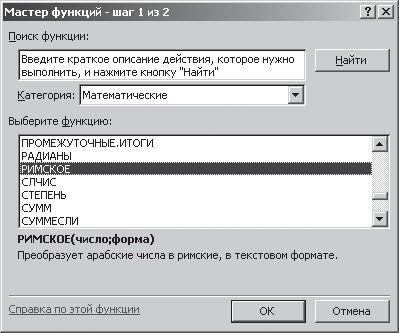
Рис. 2.2. Диалоговое окно "Мастер функций – шаг 1 из 2"
Например, число 1997 (десятичная позиционная система счисления) в римской системе счисления будет выглядеть следующим образом: MCMXCVII = 1000 + (1000 – 100) + (100 – 10) + 5 + 1 + 1. Для автоматизации процесса перевода данного числа из десятичной в римскую систему счисления воспользуемся табличным процессором MS Excel.
Для запуска программы MS Excel выполним команду: [Кнопка Пуск – Программы – MS Office ХР – Microsoft Excel]. В любую из ячеек открывшегося окна Excel введем функцию "Римское", которая и осуществит необходимый перевод. Выполним следующие действия. Выделим, например, ячейку А1 с помощью курсора и выполним следующую команду: [Вставка – Функция]. В открывшемся диалоговом окне "Мастер функций – шаг 1 из 2" (рис. 2.2), установим "Категория: Математические" и выберем функцию "Римское". После нажатия кнопки OK появится диалоговое окно "Аргументы функции", показанное на рис. 2.3. Введем число 1997 в соответствующее поле окна и нажмем кнопку OK.

Рис. 2.3. Диалоговое окно "Аргументы функции"
В результате этих действий получаем в ячейке А1 искомое значение числа 1997 в римской системе счисления (рис. 2.4).
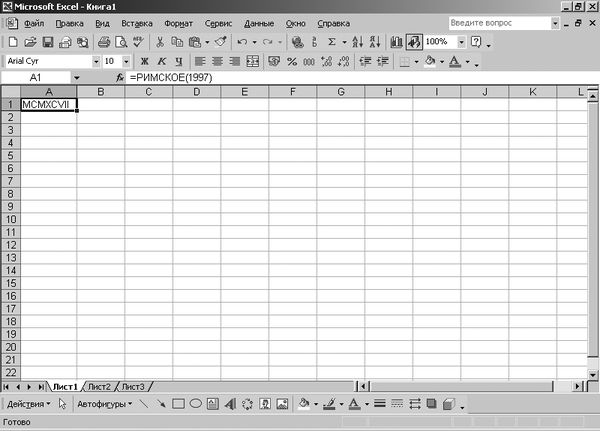
Рис. 2.4. Лист MS Excel "Результат преобразований"
Наибольшее применение при вводе, обработке и выводе информации в компьютере и компьютерных системах нашли позиционные системы счисления, при этом самыми распространенными являются десятичная, двоичная, восьмеричная и шестнадцатеричная системы. В позиционных системах счисления количественное значение цифры зависит от ее позиции в числе. Основание системы равно количеству цифр (знаков ее алфавита) и определяет, во сколько раз различаются значения цифр соседних разрядов числа. В общем случае в позиционной системе счисления любое число, содержащее целую и дробные части, в развернутой форме может быть представлено в виде:
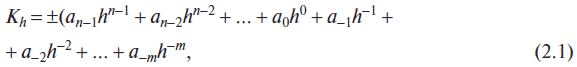
или в рекуррентной форме:

где K – представляемое число; h – основание системы счисления; а – разрядный коэффициент, а = 0, 1, 2, 3…, h-1, т. е. цифры, принадлежащие алфавиту данной системы счисления; i – номер разряда, позиция; п – число целых разрядов числа; т – число дробных разрядов числа.
В десятичной системе счисления формула (2.2) может быть записана следующим образом:

где а = 0, 1, 2, 3…, 9.
Например, число 827 десятичной системы счисления в соответствии с выражением (2.3) можно представить в виде: 827 = 8 · 10 + 2 · 10 + 7 · 10.
Десятичная система исчисления используется в компьютерах для ввода числовых данных и отображения полученного результата. Все внутренние, промежуточные операции компьютер производит в двоичной системе счисления и соотношение (2.2) примет вид: